Multi-armed bandit - wersja niestacjonarna

Ten post jest częścią moich zmagań z książką "Reinforcement Learning: An Introduction" autorstwa Richarda S. Suttona i Andrew G. Barto. Pozostałe posty systematyzujące moją wiedzę i prezentujące napisany przeze mnie kod można znaleźć pod tagiem Sutton & Barto i w repozytorium dloranc/reinforcement-learning-an-introduction.

---

Problem niestacjonarny

W tym poście zajmę się tematem szczególnego rodzaju multi-armed bandit problem (MAB), który polega na tym, że dla każdego jednorękiego bandyty wartość nagród zmienia się w czasie. Jest to tak zwana niestacjonarna wersja MAB. Do tej pory wartość nagród otrzymywana była z pewnego rozkładu normalnego o pewnej średniej i wariancji (średnia dla każdego ramienia wybierana była losowo na początku w konstruktorze).

Wyglądało to mniej więcej tak:

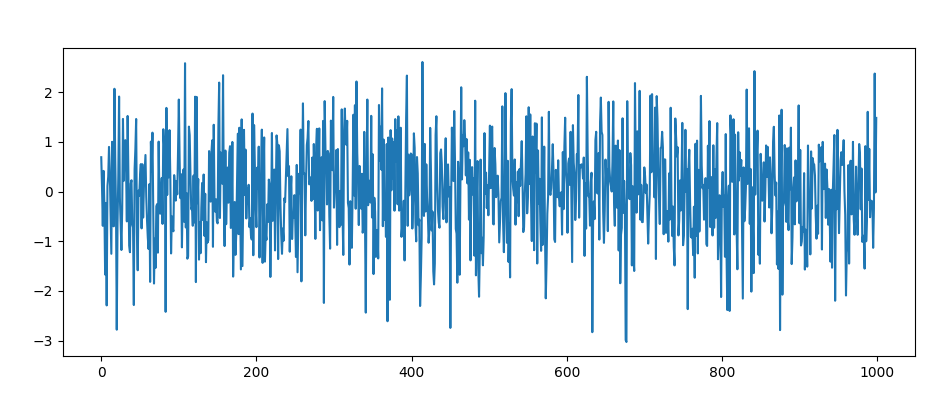
Jest to tak zwany proces stacjonarny.

Proces niestacjonarny wygląda tak i to nim się zajmiemy:

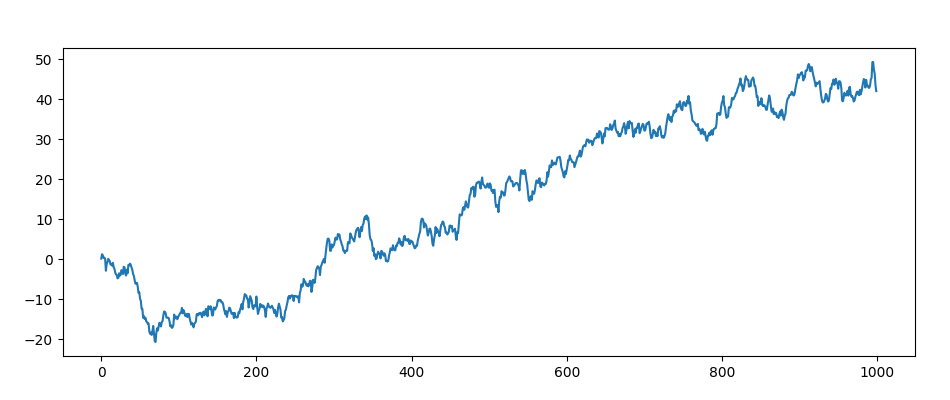
Rozwiązanie

Hmm, skoro otrzymywane nagrody zmieniają się w czasie, to będziemy potrzebowali czegoś w rodzaju średniej ważonej.

Na początek jedna rzecz, przypomnijmy wzór z poprzedniego wpisu:

$Q_{n+1} \doteq Q_n + \frac{1}{n}\Big[R_n - Q_n\Big]$

Przekształćmy go na:

$Q_{n+1} \doteq Q_n + \alpha\Big[R_n - Q_n\Big]$

Gdzie $\alpha$ będzie pewnym parametrem, mogącym mieć pewną stałą wartość albo wartość $\frac{1}{n}$ jak dotychczas.

Przekształcamy:

$$\begin{align} Q_{n+1} & \doteq Q_n + \alpha\Big[R_n - Q_n\Big] \\ & = \alpha R_n + (1 - \alpha)Q_n \\ & = \alpha R_n + (1 - \alpha)[\alpha R_{n - 1} + (1 - \alpha) Q{n - 1}] \\ & = \alpha R_n + (1 - \alpha)\alpha R_{n - 1} + (1 - \alpha)^2 Q{n - 1} \\ & = \alpha R_n + (1 - \alpha)\alpha R_{n - 1} + (1 - \alpha)^2 \alpha R_{n-2} + \\ & \qquad \qquad \dots + (1 - \alpha)^{n - 1} \alpha R_1 + (1 - \alpha)^n Q_1 \\ & = (1 - \alpha)^n + \sum_{i = 1}^n \alpha (1 - \alpha)^{n - i} R_i \end{align}$$

Podsumowanie

Sprawdźmy, czy to działa:

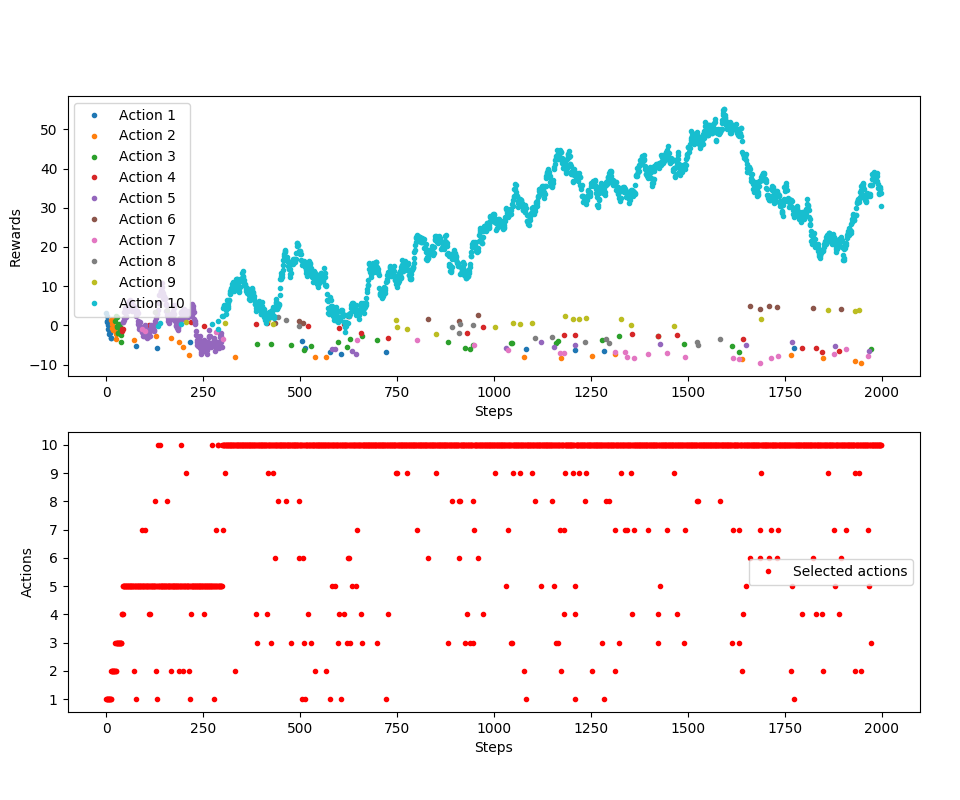
Działa. To tyle, dużo tego nie było. Trzeba było tylko znowu przerobić jedno równanie. Dodam tylko, że Sutton i Barto doradzają, by korzystać ze stałych wartości $\alpha$, gdyż sobie lepiej radzą ze względu na to, że nie spełniają pewnych warunków zbieżności szeregów i to jest akurat pożądane w niestacjonarnych problemach. Więcej szczegółów można znaleźć w książce.

Kod znajduje się tutaj. W następnym wpisie zajmę się kolejną drobną optymalizacją multi-armed bandit.