Multi-armed bandit - non-stationary version

This post is part of my struggle with the book "Reinforcement Learning: An Introduction" by Richard S. Sutton and Andrew G. Barto. Other posts systematizing my knowledge and presenting the code I wrote can be found under the tag Sutton & Barto and in the repository dloranc/reinforcement-learning-an-introduction.

---

Non-stationary problem

In this post, I will discuss a particular type of multi-armed bandit (MAB) problem, which consists in the fact that for each one-armed bandit, the value of the rewards changes over time. This is the so-called non-stationary version of MAB. Until now, the value of rewards was obtained from a certain normal distribution with a certain mean and variance (the mean for each arm was selected randomly at the beginning in the constructor).

It looked something like this:

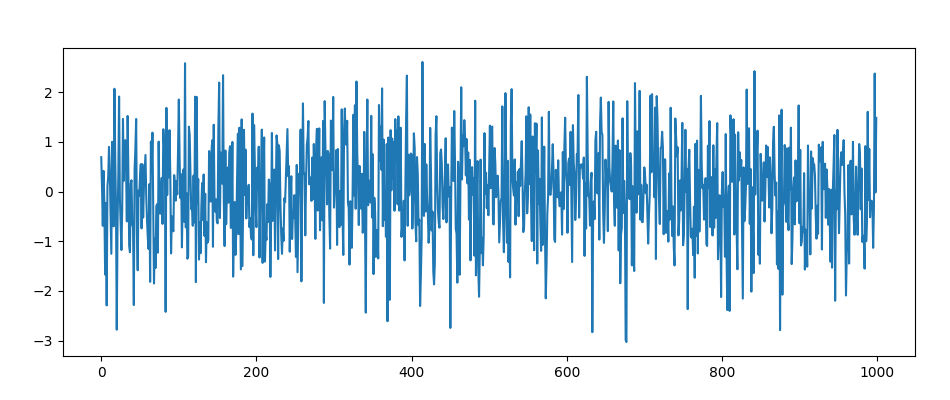
This is the so-called stationary process.

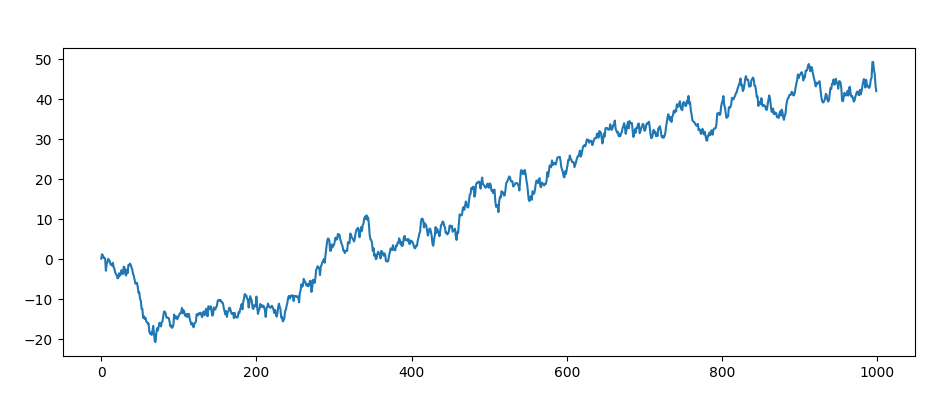
The non-stationary process looks like this and this is what we will deal with:

Solution

Hmm, since the rewards we receive change over time, we'll need something like a weighted average.

One thing first, let's recall the formula from the previous entry:

$Q_{n+1} \doteq Q_n + \frac{1}{n}\Big[R_n - Q_n\Big]$

Let's transform it to:

$Q_{n+1} \doteq Q_n + \alpha\Big[R_n - Q_n\Big]$

Where $\alpha$ will be some parameter, which may have some constant value or the value of $\frac{1}{n}$ as before.

We transform:

$$\begin{align} Q_{n+1} & \doteq Q_n + \alpha\Big[R_n - Q_n\Big] \\ & = \alpha R_n + (1 - \alpha)Q_n \\ & = \alpha R_n + (1 - \alpha)[\alpha R_{n - 1} + (1 - \alpha) Q{n - 1}] \\ & = \alpha R_n + (1 - \alpha)\alpha R_{n - 1} + (1 - \alpha)^2 Q{n - 1} \\ & = \alpha R_n + (1 - \alpha)\alpha R_{n - 1} + (1 - \alpha)^2 \alpha R_{n-2} + \\ & \qquad \qquad \dots + (1 - \alpha)^{n - 1} \alpha R_1 + (1 - \alpha)^n Q_1 \\ & = (1 - \alpha)^n + \sum_{i = 1}^n \alpha (1 - \alpha)^{n - i} R_i \end{align}$$

Summary

Sprawdźmy, czy to działa:

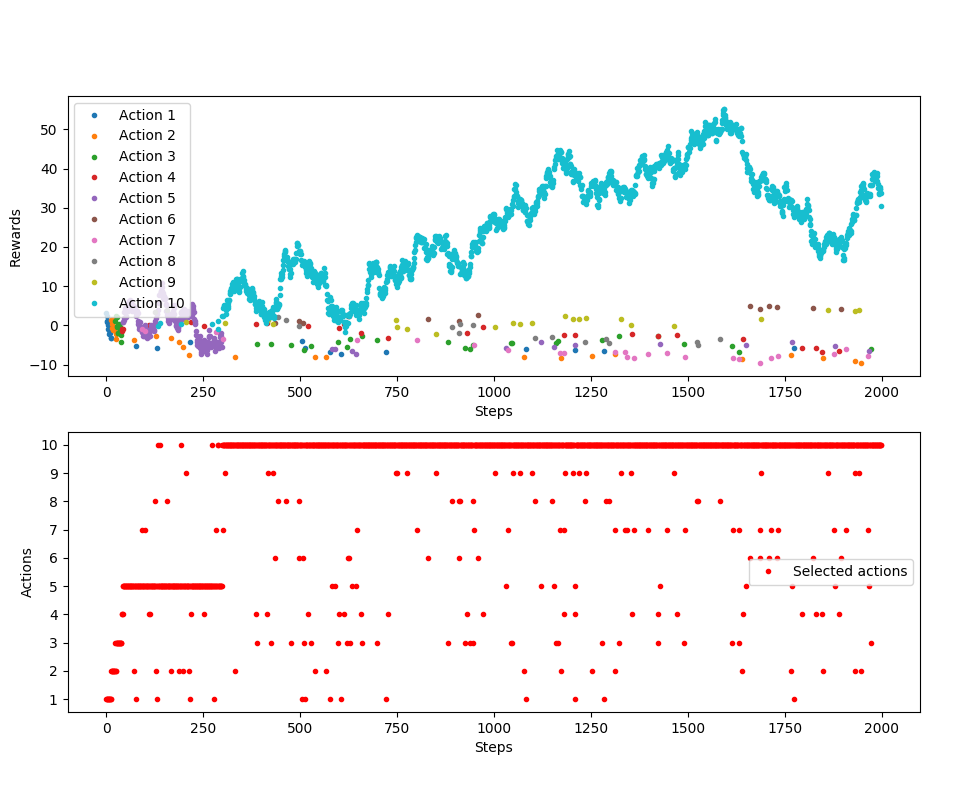
It works. That's it, it wasn't much. All we had to do was redo one equation again. I will only add that Sutton and Barto advise to use constant values ​​of $\alpha$ because they perform better due to the fact that they do not meet certain conditions for series convergence and this is desirable in non-stationary problems. More details can be found in the book.

The code is here. In the next entry I will deal with another minor optimization of multi-armed bandit.