Multi-armed bandit - Upper Confidence Bound

Ten post jest częścią moich zmagań z książką "Reinforcement Learning: An Introduction" autorstwa Richarda S. Suttona i Andrew G. Barto. Pozostałe posty systematyzujące moją wiedzę i prezentujące napisany przeze mnie kod można znaleźć pod tagiem Sutton & Barto i w repozytorium dloranc/reinforcement-learning-an-introduction.

---

W multi-armed bandit, aby znaleźć najlepszą akcję potrzebujemy eksploracji, gdyż wartość każdej akcji jest niepewna. Wartość akcji się zmienia, gdy co jakiś czas wykonujemy akcję i dowiadujemy się o otrzymanej nagrodzie. Im częściej dana akcja została wybrana, tym większą mamy pewność, że wartość tej akcji jest właściwa. Do tej pory jednak nie uwzględnialiśmy tego dość intuicyjnego spostrzeżenia w naszych obliczeniach. Akcje były wybierane losowo, bez uwzględniania tego czy wartości akcji są najbliżej tej najlepszej, bądź tego jak bardzo oszacowania są pewne.

Przypomnijmy jak wybieraliśmy najlepszą akcję:

$A_t \doteq \underset{a}{\argmax}\> Q_t(a)$

Co odpowiada tym liniom kodu:

argmax = np.argmax(self.rewards)
return argmax

Z metody choose_action:

def choose_action(self):
    rand = np.random.uniform(0, 1)

    if rand > self.epsilon:
        # exploit
        argmax = np.argmax(self.rewards)
        return argmax
    else:
        # explore
        return randint(0, self.arms - 1)

Skorzystajmy z poniższego wzoru:

$A_t \doteq \underset{a}{\argmax}\> \Bigg[Q_t(a) + c \sqrt{\frac{\log{t}}{N_t(a)}}\,\Bigg]$

Gdzie $\log{t}$ to logarytm naturalny (czyli o podstawie $e$), a $N_t(a)$ oznacza liczbę wykonanych akcji $a$.

Część z pierwiastkiem w powyższym wzorze mierzy niepewność w oszacowaniu wartości akcji $a$.

Kod wygląda następująco:

def choose_action(self):
    rand = np.random.uniform(0, 1)

    if rand > self.epsilon:
        # exploit
        ucb = self.rewards + \
            self.c * np.sqrt(np.log(self.t + 1) / (self.action_count + 1))

        return np.argmax(ucb)
    else:
        # explore
        return randint(0, self.arms - 1)

W konstruktorze dodałem c i t:

def __init__(self, arms, pulls, epsilon, c=0):
    self.t = 0
    self.c = c

c jest parametrem, który kontroluje stopień eksploracji.

Wygenerowałem tabelkę z możliwymi wartościami dla jakiejś akcji $a$:

$t$	$N_t$	$\log{t}$	$c\sqrt{\frac{\log{t}}{N_t}}, c = 2$
1	1	0	0
2	1	0,3010299957	1,0973240099
3	1	0,4771212547	1,3814792864
4	1	0,6020599913	1,5518504971
5	1	0,6989700043	1,6720885196
6	2	0,7781512504	1,2475185372
7	2	0,84509804	1,3000754132
8	2	0,903089987	1,3439419534
9	2	0,9542425094	1,3814792864
10	2	1	1,4142135624
11	3	1,0413926852	1,1783563044
12	3	1,079181246	1,1995450505
13	3	1,1139433523	1,218711534
14	3	1,1461280357	1,2361920216
15	3	1,1760912591	1,2522466525
16	4	1,2041199827	1,0973240099
17	4	1,2304489214	1,1092560216
18	4	1,2552725051	1,1203894435
19	4	1,278753601	1,13081988
20	4	1,3010299957	1,1406270186
21	5	1,3222192947	1,0284821028
22	5	1,3424226808	1,036309869
23	5	1,361727836	1,0437347694
24	5	1,3802112417	1,0507944582
25	5	1,3979400087	1,0575216343
26	6	1,414973348	0,9712443386
27	6	1,4313637642	0,9768533715
28	6	1,4471580313	0,9822280901
29	6	1,4623979979	0,9873864485
30	6	1,4771212547	0,9923444478
31	7	1,4913616938	0,9231504115
32	7	1,5051499783	0,9274080558
33	7	1,5185139399	0,9315161036
34	7	1,531478917	0,9354842648
35	7	1,5440680444	0,939321349
36	8	1,5563025008	0,8821288173
37	8	1,5682017241	0,885494699
38	8	1,5797835966	0,8887585714
39	9	1,591064607	0,8409160632
40	10	1,6020599913	0,8005148322
41	11	1,6127838567	0,7658112411
42	12	1,6232492904	0,7355835077
43	13	1,6334684556	0,70894688
44	14	1,6434526765	0,6852429551
45	15	1,6532125138	0,6639703836
46	16	1,6627578317	0,6447398374
47	17	1,6720978579	0,6272438044
48	18	1,6812412374	0,6112357678
49	19	1,69019608	0,59651551
50	20	1,6989700043	0,5829185199
51	21	1,7075701761	0,5703082168
52	22	1,7160033436	0,5585701459
53	23	1,7242758696	0,5476075824
54	24	1,7323937598	0,5373381555
55	25	1,7403626895	0,5276912263
56	26	1,748188027	0,5186058273
57	27	1,7558748557	0,5100290269
58	28	1,7634279936	0,501914619
59	29	1,7708520116	0,4942220654

Jak widać po wartościach z tabelki, wraz z upływem czasu $t$ ogólnie wartość niepewności w pierwiastku maleje, ale jeśli akcja nie była wybierana, to niepewność nieco wzrasta.

Podsumowanie

Sposób takiego wybierania akcji w zależności od niepewności oznacza się skrótem UCB (upper confidence bound). Jest to metoda statystyczna związana z przedziałami ufności, a przynajmniej tak to rozumiem. Mało co już pamiętam ze statystyki, nigdy nie byłem w niej dobry. UCB jest to całkiem dobra metoda, ale Sutton & Barto ostrzegają, że słabo się sprawdza w problemach niestacjonarnych albo w problemach, w których mamy do czynienia z dużą przestrzenią stanu (large state space, dobrze to przetłumaczyłem na polski?).

Kod można zobaczyć tutaj.

Na sam koniec jeszcze wykresy:

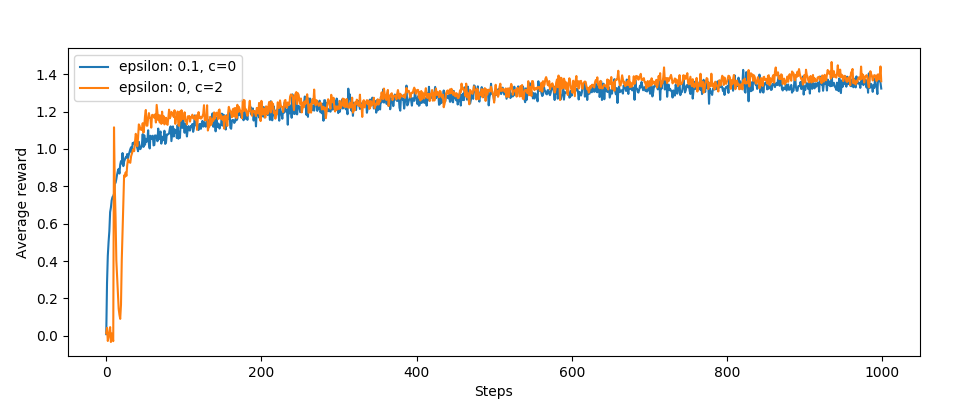
Całkiem nieźle, średnio UCB wypada lepiej od wersji bez jeśli chodzi o średnie nagrody. Interesujący jest ten skok i spadek na początku działania algorytmu.

Z optymalnymi akcjami jest gorzej:

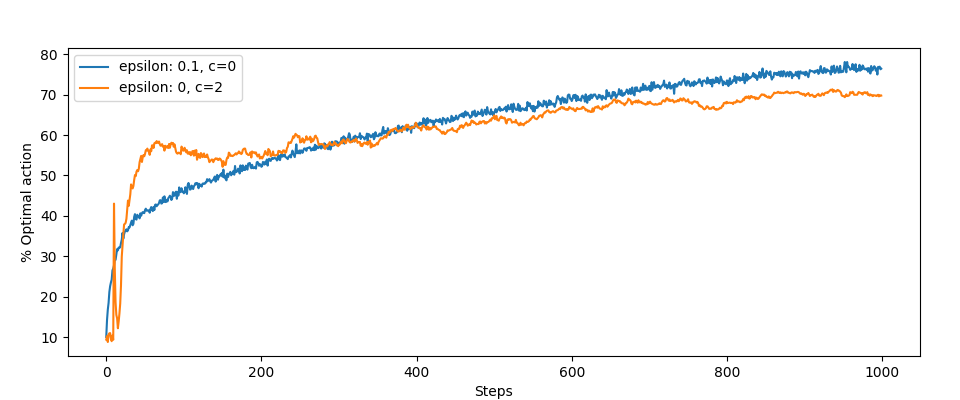
Nic dziwnego, eksploracja zachodzi częściej.

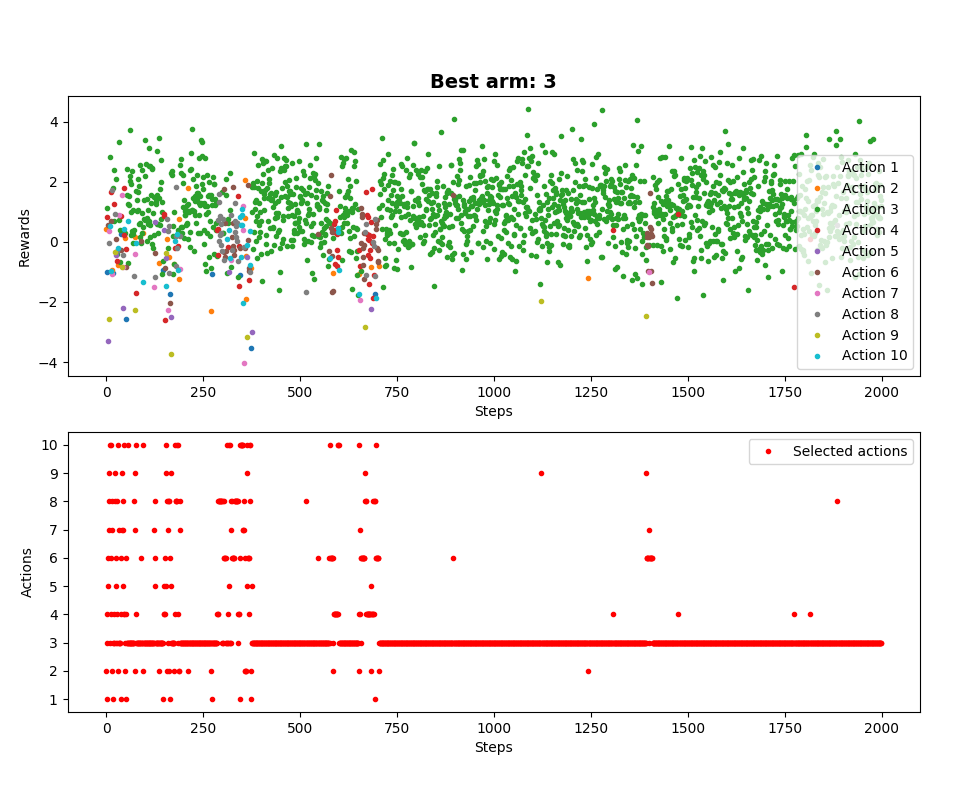
Dla jednego przebiegu MAB: