Multi-armed bandit - Upper Confidence Bound

May 31, 2017 · 6 min read

This post is part of my struggle with the book "Reinforcement Learning: An Introduction" by Richard S. Sutton and Andrew G. Barto. Other posts systematizing my knowledge and presenting the code I wrote can be found under the tag Sutton & Barto and in the repository dloranc/reinforcement-learning-an-introduction.

In multi-armed bandit we need exploration to find the best action because the value of each action is uncertain. The value of the action changes when we perform the action from time to time and learn about the reward we receive. The more often a given action is selected, the more certain we are that the value of this action is correct. So far, however, we have not taken this rather intuitive observation into account in our calculations. The actions were selected randomly, without taking into account whether the action values were closest to the best one or how certain the estimates were.

Let's recall how we chose the best action:

$A_t \doteq \underset{a}{\argmax}\> Q_t(a)$

Which corresponds to these lines of code:

argmax = np.argmax(self.rewards)
return argmax

From the choose_action method:

def choose_action(self):
    rand = np.random.uniform(0, 1)

    if rand > self.epsilon:
        # exploit
        argmax = np.argmax(self.rewards)
        return argmax
    else:
        # explore
        return randint(0, self.arms - 1)

Let's use the formula below:

$A_t \doteq \underset{a}{\argmax}\> \Bigg[Q_t(a) + c \sqrt{\frac{\log{t}}{N_t(a)}}\,\Bigg]$

Where $\log{t}$ is the natural logarithm (i.e. to the base of the $e$ constant), and $N_t(a)$ is the number of $a$ actions performed.

The square root part of the above formula measures the uncertainty in the estimate of the value of the stock $a$ .

The code looks like this:

def choose_action(self):
    rand = np.random.uniform(0, 1)

    if rand > self.epsilon:
        # exploit
        ucb = self.rewards + \
            self.c * np.sqrt(np.log(self.t + 1) / (self.action_count + 1))

        return np.argmax(ucb)
    else:
        # explore
        return randint(0, self.arms - 1)

In the constructor I added c and t:

def __init__(self, arms, pulls, epsilon, c=0):
    self.t = 0
    self.c = c

c is a parameter that controls the degree of exploration.

I generated a table with possible values for some $a$ action:

$t$	$N_t$	$\log{t}$	$c\sqrt{\frac{\log{t}}{N_t}}, c = 2$
1	1	0	0
2	1	0,3010299957	1,0973240099
3	1	0,4771212547	1,3814792864
4	1	0,6020599913	1,5518504971
5	1	0,6989700043	1,6720885196
6	2	0,7781512504	1,2475185372
7	2	0,84509804	1,3000754132
8	2	0,903089987	1,3439419534
9	2	0,9542425094	1,3814792864
10	2	1	1,4142135624
11	3	1,0413926852	1,1783563044
12	3	1,079181246	1,1995450505
13	3	1,1139433523	1,218711534
14	3	1,1461280357	1,2361920216
15	3	1,1760912591	1,2522466525
16	4	1,2041199827	1,0973240099
17	4	1,2304489214	1,1092560216
18	4	1,2552725051	1,1203894435
19	4	1,278753601	1,13081988
20	4	1,3010299957	1,1406270186
21	5	1,3222192947	1,0284821028
22	5	1,3424226808	1,036309869
23	5	1,361727836	1,0437347694
24	5	1,3802112417	1,0507944582
25	5	1,3979400087	1,0575216343
26	6	1,414973348	0,9712443386
27	6	1,4313637642	0,9768533715
28	6	1,4471580313	0,9822280901
29	6	1,4623979979	0,9873864485
30	6	1,4771212547	0,9923444478
31	7	1,4913616938	0,9231504115
32	7	1,5051499783	0,9274080558
33	7	1,5185139399	0,9315161036
34	7	1,531478917	0,9354842648
35	7	1,5440680444	0,939321349
36	8	1,5563025008	0,8821288173
37	8	1,5682017241	0,885494699
38	8	1,5797835966	0,8887585714
39	9	1,591064607	0,8409160632
40	10	1,6020599913	0,8005148322
41	11	1,6127838567	0,7658112411
42	12	1,6232492904	0,7355835077
43	13	1,6334684556	0,70894688
44	14	1,6434526765	0,6852429551
45	15	1,6532125138	0,6639703836
46	16	1,6627578317	0,6447398374
47	17	1,6720978579	0,6272438044
48	18	1,6812412374	0,6112357678
49	19	1,69019608	0,59651551
50	20	1,6989700043	0,5829185199
51	21	1,7075701761	0,5703082168
52	22	1,7160033436	0,5585701459
53	23	1,7242758696	0,5476075824
54	24	1,7323937598	0,5373381555
55	25	1,7403626895	0,5276912263
56	26	1,748188027	0,5186058273
57	27	1,7558748557	0,5100290269
58	28	1,7634279936	0,501914619
59	29	1,7708520116	0,4942220654

As can be seen from the values in the table, with the passage of time $t$ , the uncertainty value in the root generally decreases, but if the action was not selected, the uncertainty increases slightly.

Summary

This method of selecting shares depending on uncertainty is abbreviated as UCB (upper confidence bound). This is a statistical method related to confidence intervals, or at least that's how I understand it. I barely remember anything about statistics, I was never good at it. UCB is quite a good method, but Sutton & Barto warn that it does not work well in non-stationary problems or in problems in which we are dealing with a large state space.

The code can be seen here.

Finally, some charts:

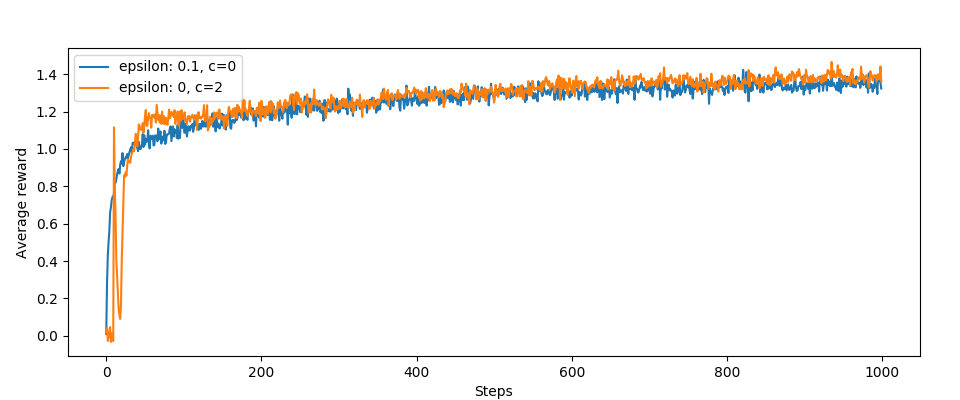
average rewards

Pretty good, on average UCB is better than the version without it in terms of average rewards. This jump and drop at the beginning of the algorithm is interesting.

It's worse with optimal actions:

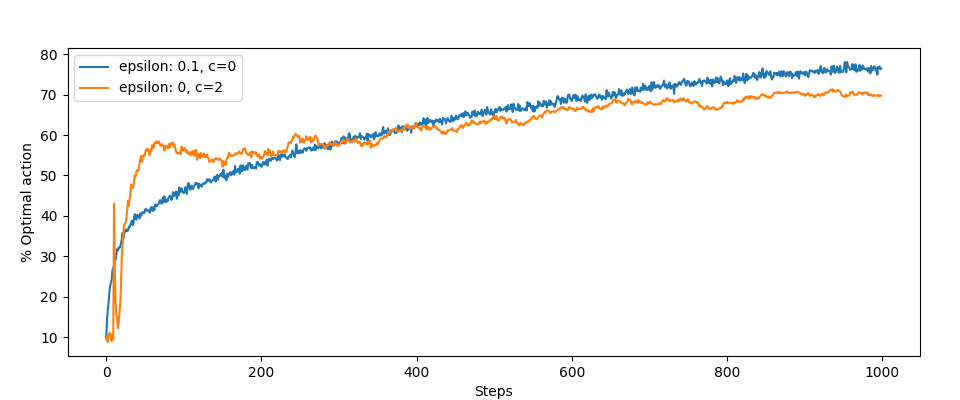
No wonder, exploration happens more often.

For one MAB run:

Summary​

Summary