Multi-armed bandit - optymistyczne wartości początkowe

28 maja 2017 · 3 min aby przeczytać

Ten post jest częścią moich zmagań z książką "Reinforcement Learning: An Introduction" autorstwa Richarda S. Suttona i Andrew G. Barto. Pozostałe posty systematyzujące moją wiedzę i prezentujące napisany przeze mnie kod można znaleźć pod tagiem Sutton & Barto i w repozytorium dloranc/reinforcement-learning-an-introduction.

Wszystkie metody, które do tej pory opisałem zależne są od początkowych oszacowań wartości $Q_1(a)$ . Widoczne to jest zwłaszcza, gdy liczymy MAB z $\epsilon = 0$ , czyli bez ekploracji cały czas wybierając najlepszą możliwą akcję (ramię). W statystyce nazywamy takie metody obciążonymi. Obciążenie znika dla metod z $\alpha$ wynoszącym $\frac{1}{n}$ , gdy każda akcja zostanie wybrana co najmniej raz. Dla stałego $\alpha$ , obciążenie nie znika, zmniejsza się jedynie wraz z upływem czasu (kolejnymi iteracjami algorytmu).

Aby pozbyć się obciążenia, możemy skorzystać z czegoś takiego jak optymistyczne wartości początkowe. W kodzie przykładów jakie do tej pory napisałem prawdziwe wartości każdej akcji (true value), pochodziły z rozkładu normalnego (średnia 0, wariancja 1) i ustalane były w konstruktorze:

self.true_reward = [np.random.randn() for _ in range(self.arms)]

Przy okazji przypominam, że pobieranie wartości dla danej akcji wygląda tak:

def get_reward(self, action):
    return self.true_reward[action] + np.random.randn()

To tyle celem przypomnienia.

Możemy na początku działania zachęcić algorytm do eksploracji ustalając bardzo optymistyczne wartości początkowe. Ja wybrałem liczbę 5 i wygląda to tak:

self.action_count = np.ones(self.arms)

self.rewards = np.ones(self.arms) * 5

I to wszystko, więcej modyfikacji w kodzie nie trzeba. Co się dzieje jak odpalimy skrypt z takimi wartościami self.rewards? Zobaczmy to na przykładzie z epsilonem równym zero:

self.rewards:
[ 5.  5.  5.  5.  5.  5.  5.  5.  5.  5.]

reward: 1.87411213524
[ 3.43705607  5.          5.          5.          5.          5.          5.
  1.          5.          5.        ]
reward: 0.504446069392
[ 3.43705607  2.75222303  5.          5.          5.          5.          5.
  1.          5.          5.        ]
reward: 0.374953664141
[ 3.43705607  2.75222303  2.68747683  5.          5.          5.          5.
  1.          5.          5.        ]
reward: -3.66371477543
[ 3.43705607  2.75222303  2.68747683  0.66814261  5.          5.          5.
  1.          5.          5.        ]
reward: -1.59327852639
[ 3.43705607  2.75222303  2.68747683  0.66814261  1.70336074  5.          5.
  1.          5.          5.        ]
reward: -2.41539982786
[ 3.43705607  2.75222303  2.68747683  0.66814261  1.70336074  1.29230009
  1.          5.          5.          5.        ]
reward: -0.641184621377
[ 3.43705607  2.75222303  2.68747683  0.66814261  1.70336074  1.29230009
  2.17940769  5.          5.          5.        ]
reward: -1.53850026836
[ 3.43705607  2.75222303  2.68747683  0.66814261  1.70336074  1.29230009
  2.17940769  1.73074987  5.          5.        ]

Otrzymane nagrody są niższe niż pięć, a do tego uśredniane, więc nawet dla epsilona wynoszącego zero następuje eksploracja i algorytm po kolei próbuje każdej akcji. Zobaczmy to jeszcze w formie graficznej (epsilon równy zero):

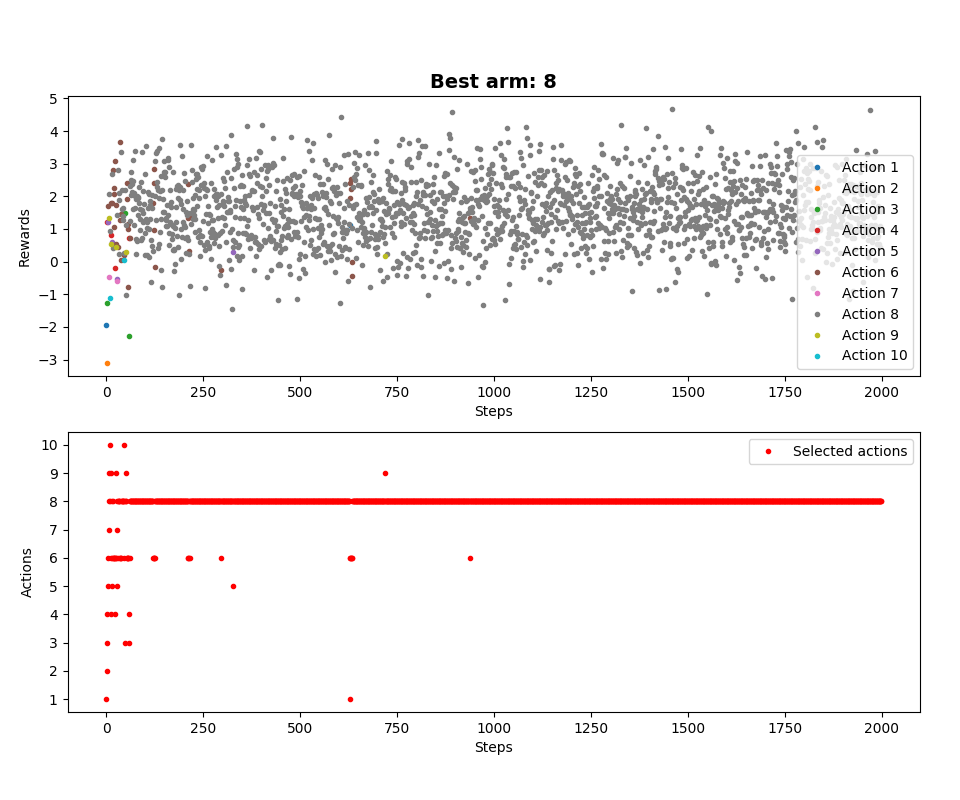
optimistic initial values, epsilon = 0

Dla porównania, bez naszej optymalizacji (epsilon również wynosi zero):

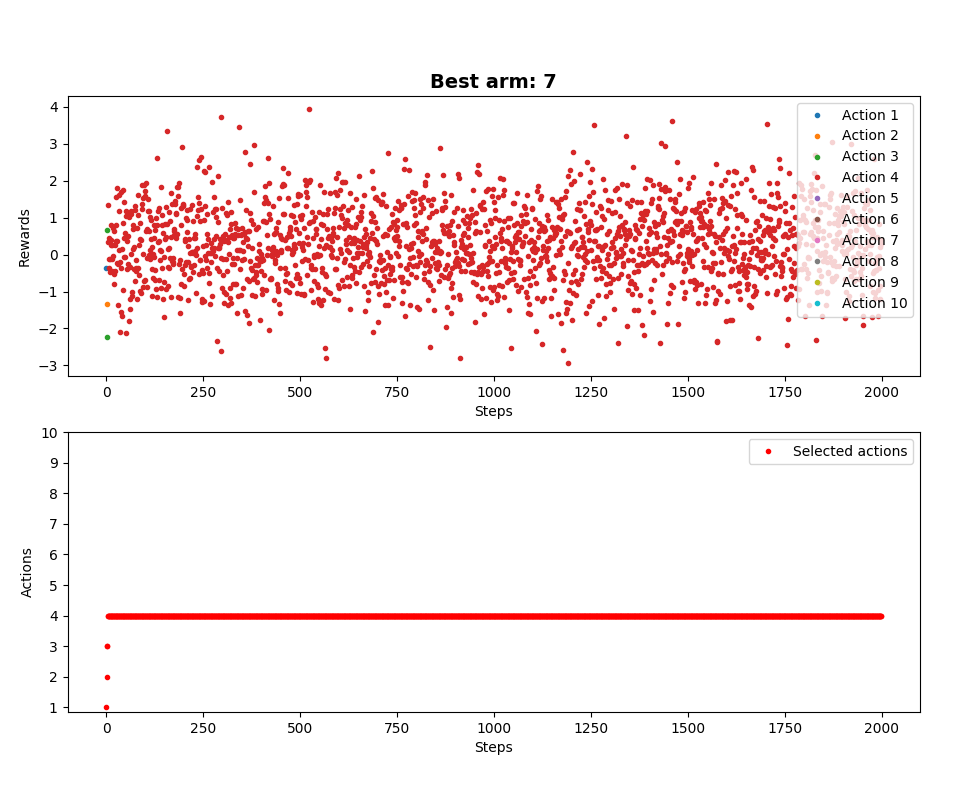
bez optimistic initial values, epsilon = 0

Inne wykresy, te skoki na początku są interesujące. Jest to efekt działania naszej optymalizacji:

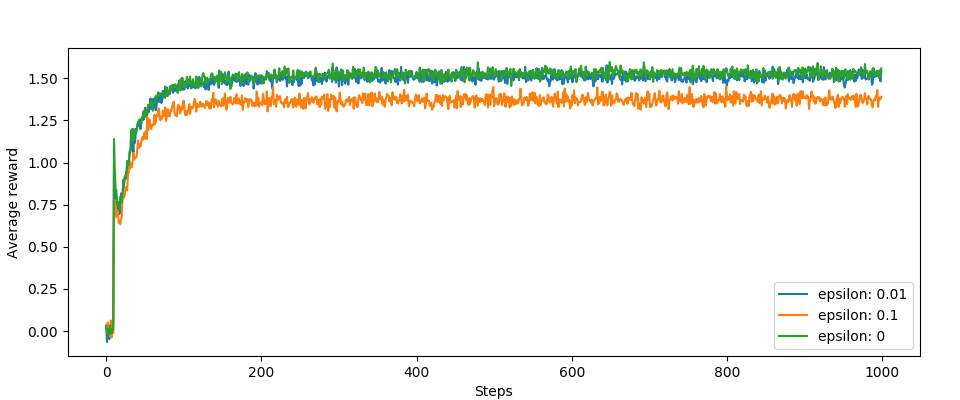
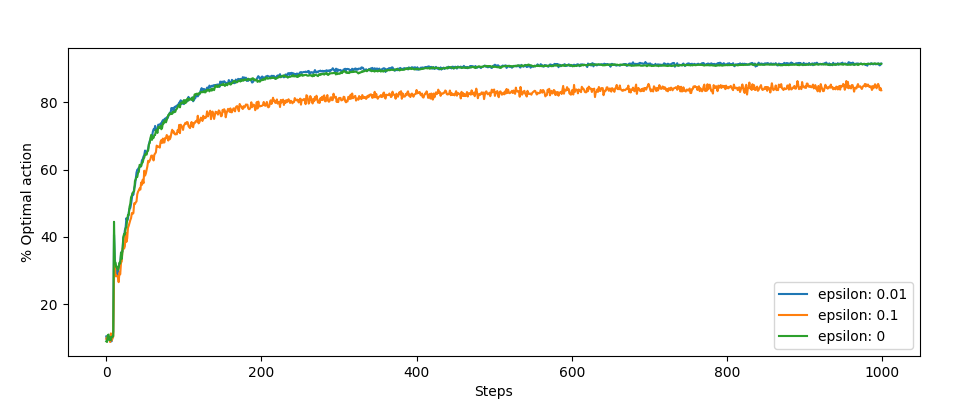
średnie nagrody optymalne akcje

Podsumowanie

Jak widać, jest to prosty, ale dość skuteczny sposób, by zachęcić MAB z e-greedy strategy, nawet gdy wybiera najlepsze akcje za każdym razem. Sposób ten jednak działa tylko na początku algorytmu, przy pierwszych kilkunastu iteracjach. W następnym poście zajmę się sposobem na ulepszenie eksploracji, tak zwanym Upper-Confidence-Bound (jak to przetłumaczyć?).

Podsumowanie​

Podsumowanie